domingo, 10 de noviembre de 2013
martes, 1 de octubre de 2013
factorizacion
FACTORIZACION.
En matemáticas, la factorización (o factoreo) es una técnica que consiste la descomposición de una expresión matemática (que puede ser un número, una suma, una matriz, un polinomio, etc) en forma de multiplicación. Existen diferentes métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que reciben el nombre de factores, como por ejemplo un número en números primos, o un polinomio en polinomios irreducibles.
El teorema fundamental de la aritmética cubre la factorización de números enteros, y para la factorización de polinomios, el teorema fundamental del álgebra. La factorización de números enteros muy grandes en producto de factores primos requiere de algoritmos sofisticados, el nivel de complejidad de tales algoritmos está a la base de la fiabilidad de algunos sistemas de criptografia asimétrica.
existen casos de factorizacion:

biografías:
la historia de la factorizacion:
La factorización ha sido un tema del cual han tratado numerosos matemáticos importantes, haciendo un recorrido por la historia de las matemáticas, específicamente con la solución de ecuaciones polinómicas con coeficientes racionales.
La factorización es una de las herramientas más empleadas en el trabajo matemático para “transformar” una expresión algebraica de manera conveniente, para resolver algún problema.
Tiene una importancia apreciable a través de la historia, es la solución de ecuaciones algebraicas; de hecho, en un primer momento, la factorización surge ante la
necesidad de solucionar ecuaciones de segundo grado.
Los babilonios, fueron los primeros que resolvieron, ecuaciones cuadráticas
En unas tablillas descifradas por Neugebauer 1930, cuya antigüedad es
de unos 4000 años, se encontraron soluciones a varias de estas ecuaciones, empleando el método conocido actualmente como “completar el cuadrado”.
Hace unos 4.000 años, los babilonios conocían la manera de encontrar la solución positiva de ciertos tipos de ecuaciones cuadráticas. Tenían una "receta" muy precisa para resolver ecuaciones del tipo
El trabajo de los babilonios constituyó un logro notable, teniendo en cuenta que no contaban con la notación moderna y por su alto nivel de abstracción, al considerar las ecuaciones cuárticas como ecuaciones cuadráticas “disfrazadas” y resolverlas como tales.
Más adelante, matemáticos griegos, hindúes, árabes y europeos se dedicaron al estudio de estas ecuaciones y lograron avanzar a través del tiempo hasta encontrar la fórmula para resolver cualquier ecuación de segundo grado, es decir, una ecuación de la forma
la historia de la factorizacion:
La factorización ha sido un tema del cual han tratado numerosos matemáticos importantes, haciendo un recorrido por la historia de las matemáticas, específicamente con la solución de ecuaciones polinómicas con coeficientes racionales.
La factorización es una de las herramientas más empleadas en el trabajo matemático para “transformar” una expresión algebraica de manera conveniente, para resolver algún problema.
Tiene una importancia apreciable a través de la historia, es la solución de ecuaciones algebraicas; de hecho, en un primer momento, la factorización surge ante la
necesidad de solucionar ecuaciones de segundo grado.
Los babilonios, fueron los primeros que resolvieron, ecuaciones cuadráticas
En unas tablillas descifradas por Neugebauer 1930, cuya antigüedad es
de unos 4000 años, se encontraron soluciones a varias de estas ecuaciones, empleando el método conocido actualmente como “completar el cuadrado”.
Hace unos 4.000 años, los babilonios conocían la manera de encontrar la solución positiva de ciertos tipos de ecuaciones cuadráticas. Tenían una "receta" muy precisa para resolver ecuaciones del tipo
El trabajo de los babilonios constituyó un logro notable, teniendo en cuenta que no contaban con la notación moderna y por su alto nivel de abstracción, al considerar las ecuaciones cuárticas como ecuaciones cuadráticas “disfrazadas” y resolverlas como tales.
Más adelante, matemáticos griegos, hindúes, árabes y europeos se dedicaron al estudio de estas ecuaciones y lograron avanzar a través del tiempo hasta encontrar la fórmula para resolver cualquier ecuación de segundo grado, es decir, una ecuación de la forma
NEUGEBAUER:Otto E. Neugebauer (* 26 de mayo de 1899 en Innsbruck; † 19 de febrero de 1990) fue un matemático y astrónomo austriaco-estadounidense dedicado exclusivamente a la investigación de la historia de la ciencia, y en especial de la Astronomía. Fue un investigador tenaz, y el gran descubridor de la matemática babilónica. Ganó el Premio Balzan en 1986 para la historia de la ciencia.
FACTOR COMUN:
Es el primer paso que se utiliza para factorizar un polinomio
FACTOR COMUN:
Es el primer paso que se utiliza para factorizar un polinomio
-El factor debe estar en todos los términos que compone el polinomio
-En las variables,sacar la base con el menor exponente
-En los números,sacar el mayor factor entre ellos
-Se multiplica el factor común por el polinomio
DIFERENCIA DE CUADRADOS:
-Se utiliza cuando hay un binomio,Cuando los dos terminos son cuadrados perfectos y en medio de los dos terminos hay una resta
-Se factoriza sacando la raiz cuadrada de cada termino
-Formar dos binomios uno de suma y otro de resta de las raices cuadradas,multiplicandose entre si
DIFERENCIA DE CUBOS:
Se utiliza cuando hay un binomio, cuando los dos terminos son cubos perfectos y en medio de los dos terminos hay una resta
-Se factoriza sacando la raiz cubica de cada termino, estos van a formar un binomio con resta, que van a multiplicar un trinomio conformado por el cuadrado de la primera raiz,mas el producto entre las dos raices,mas la ultima raiz al cuadrado
SUMA DE CUBOS:
Se utiliza cuando hay un binomio,cuando los dos terminos son cubos perfectos y en medio de los dos hay una suma
-Se factoriza sacando la raiz cubica de cada termino, estos van a formar un binomio con suma, que van a multiplicar un trinomio conformado por el cuadrado de la primera raiz,menos el producto entre las dos raices,mas la ultima raiz al cuadrado
-En las variables,sacar la base con el menor exponente
-En los números,sacar el mayor factor entre ellos
-Se multiplica el factor común por el polinomio
DIFERENCIA DE CUADRADOS:
-Se utiliza cuando hay un binomio,Cuando los dos terminos son cuadrados perfectos y en medio de los dos terminos hay una resta
-Se factoriza sacando la raiz cuadrada de cada termino
-Formar dos binomios uno de suma y otro de resta de las raices cuadradas,multiplicandose entre si
DIFERENCIA DE CUBOS:
Se utiliza cuando hay un binomio, cuando los dos terminos son cubos perfectos y en medio de los dos terminos hay una resta
-Se factoriza sacando la raiz cubica de cada termino, estos van a formar un binomio con resta, que van a multiplicar un trinomio conformado por el cuadrado de la primera raiz,mas el producto entre las dos raices,mas la ultima raiz al cuadrado
SUMA DE CUBOS:
Se utiliza cuando hay un binomio,cuando los dos terminos son cubos perfectos y en medio de los dos hay una suma
-Se factoriza sacando la raiz cubica de cada termino, estos van a formar un binomio con suma, que van a multiplicar un trinomio conformado por el cuadrado de la primera raiz,menos el producto entre las dos raices,mas la ultima raiz al cuadrado
TRINOMIO CUADRADO PERFECTO:
Se utliza cuando hay un trinomio, cuando el primer y ultimo termino son cuadrados perfectos y positivos,el segundo termino es el doble de producto de las raices cuadradas de los terminos cuadrados perfectos
-Se factoriza sacando la raiz cuadrada de cada termino cuadrado perfecto
-Se forma una resta de las dos raices cuadradas elevadas al cuadrado,si el segundo termino del trinomio es negativo se forma una suma de las dos raices cuadradas elevada al cuadrado, si el segundo termino del trinomio es positivo
lunes, 26 de agosto de 2013
martes, 20 de agosto de 2013
polinomio entre polinomio
Para
dividir dos polinomios se procede de la manera siguiente:
1) Se
ordena el dividendo y el divisor con
respecto a una misma letra.
2) Se divide
el primer término del dividendo entre el primer término del divisor,
obteniéndose así el primer término del cociente
3) Se
multiplica el primer término del cociente por todo el divisor y el producto así
obtenido se resta del dividendo, para lo cual se le cambia de signo y se
escribe cada término de su semejante. En el caso de que algún término de este
producto no tenga ningún término semejante en el dividendo, es escribe dicho
término en el lugar que le corresponda de acuerdo con la ordenación del
dividendo y del divisor.
4) Se
divide el primer término del resto entre el primer término del divisor,
obteniéndose de este modo el segundo término del cociente.
5) El
segundo término del cociente se
multiplica por todo el divisor y el producto así obtenido se resta del
dividendo, cambiándole todos los signos.
6) Se
divide el primer término del segundo resto entre el primer término del
divisor y se repiten las operaciones anteriores hasta obtener cero como resto.
Dividir:


jueves, 8 de agosto de 2013
division entre polinomios.
monomio por monomio:
se divide el cociente y se resta el exponente compatible si no hay ningún exponente compatible se agrega al resultado
http://www.youtube.com/watch?v=egeSGTrbtnY&feature=youtu.be
en el ejemplo y el video se explica mejor
aqui podemos ver las partes de la division esto nos ayuda a entenderla mejor
Biografia
BIOGRAFÍA:
Aristóteles:
Aristóteles:
- Aristóteles fue un polímata: filósofo, lógico y científico de la Antigua Grecia cuyas ideas han ejercido una enorme influencia sobre la historia intelectual de Occidente por más de dos milenios. WikipediaFecha de nacimiento: 384 a.C., Estagira, GreciaFecha de la muerte: 322 a.C., Calcis, GreciaEducación: Academia de Atenas (367 a.C.–347 a.C.)
el se destaco por
miércoles, 19 de junio de 2013
estadistica
estadística
La estadística es una ciencia formal que estudia la recolección, análisis e interpretación de datos de una muestra representativa, ya sea para ayudar en la toma de decisiones o para explicar condiciones regulares o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma aleatoria o condicional.
gráfico circular

gratifico de barras

ojiva

tabla de frecuencias

La estadística es una ciencia formal que estudia la recolección, análisis e interpretación de datos de una muestra representativa, ya sea para ayudar en la toma de decisiones o para explicar condiciones regulares o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma aleatoria o condicional.
gráfico circular

gratifico de barras

ojiva

tabla de frecuencias

sábado, 18 de mayo de 2013
II BIMESTRE
POLINOMIO POR POLINOMIO:
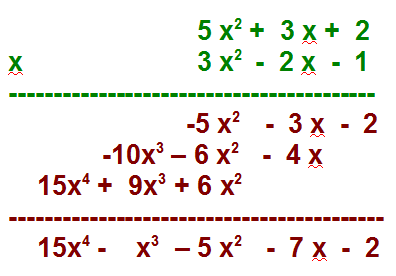
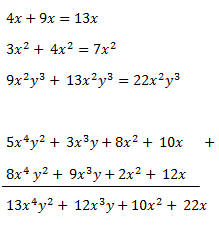
 ya se que no vimos todo esto pero quería tener mas información para el blog
ya se que no vimos todo esto pero quería tener mas información para el blog

gráfico de varas:se dibuja una baras con respecto al valor deseado se hace con cualquier tipo de frecuencias

histograma:es lo mismo que el gráfico de baras sino que este debe estar estrictamente pegado

pictograma:es un gráfico de baras pero con dibujos con respecto a lo que se trata

gráfico de lineas:se realiza común mente con la fi o al respecto de la ojiva que es lo mismo con la fi agrupada

se gráfica por medio de putos correspondientes al valor de lo que se pide y después unirlos con lineas
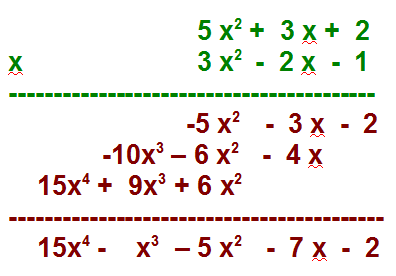
MONOMIO POR MONOMIO:
Cada uno de los términos de una multiplicación se llama factores y su resultado se llama producto de los factores. Para multiplicar dos monomios realizamos los siguientes pasos:
-Multiplicar signos usando la ley
-Multiplicar los coeficientes numéricos
-Multiplicar las variables iguales usando la regla de producto
-Escribir las variables diferentes
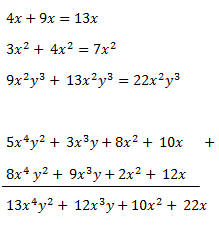
MONOMIO POR POLINOMIO:
Para multiplicar un monomio por un polinomio se deben realizar los siguientes pasos:
-Multiplicar el monomio por el primer termino
-Multiplicar el monomio por el termino siguiente
-Repetir el segundo paso hasta multiplicar todos los términos
-Reducir términos semejantes si es posible
área de un rectángulo y triangulo
rectángulo: base X altura
triangulo: base X altura / dos
para mas información favor de ver lo vídeos 2 bimestre
en el vídeo esta incluido multiplicación polinomio por polinomio
productos notables:
área de un rectángulo y triangulo
rectángulo: base X altura
triangulo: base X altura / dos
para mas información favor de ver lo vídeos 2 bimestre
en el vídeo esta incluido multiplicación polinomio por polinomio
productos notables:
video 1: estos videos te ayudaran a entender mejor el tema
productos notables:

estadística:
pipe ponga su vídeo aquí y yo complemento lo demás
gráficas:
circular :este se hace con la hi y se saca la porcion de el circulo utilizando regla de 3

gráfico de varas:se dibuja una baras con respecto al valor deseado se hace con cualquier tipo de frecuencias
histograma:es lo mismo que el gráfico de baras sino que este debe estar estrictamente pegado
pictograma:es un gráfico de baras pero con dibujos con respecto a lo que se trata
gráfico de lineas:se realiza común mente con la fi o al respecto de la ojiva que es lo mismo con la fi agrupada
se gráfica por medio de putos correspondientes al valor de lo que se pide y después unirlos con lineas
Suscribirse a:
Entradas (Atom)